L’alterità come limite

Interpretazione matematica del concetto di alterità in Jean-Paul Sartre

Il limite è, genericamente, il valore cui si approssima indefinitamente una funzione, una serie o una successione. In ambito d’analisi matematica, nello specifico dello studio di funzioni, il concetto di limite viene utilizzato in merito a una particolare procedura che stabilisce la presenza di asintoti, questi ultimi preziosi per capire l’andatura di una curva geometrica. L’asintoto si definisce come la tangente a una curva piana in un suo punto all’infinito, ossia come la posizione limite, assunta dalla tangente alla curva, quando il punto tende all’infinito. Parafrasando il tutto con una terminologia più accessibile, possiamo semplicemente dire che l’asintoto è quella retta che una curva segue indefinitamente, avvicinandovisi, senza però mai ‘toccarla’.

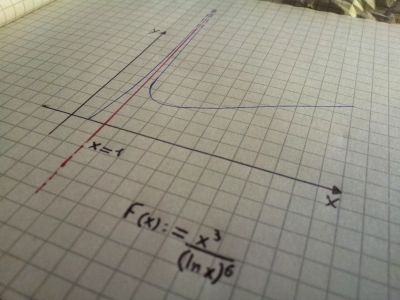Considerando intuitivamente la rappresentazione grafica della funzione, essa presenta – per sua essenza – un’asintoticità costitutiva. Come si può notare, l’asintoto verticale (in rosso) spezza letteralmente la funzione in due curve, entrambe a lui asintotiche, le quali, perciò, lo seguiranno all’infinito senza mai raggiungerlo, pur quasi sfiorandolo. Immaginiamo che le due curve (in blu) rappresentino rispettivamente me e altri e che un nulla di separazione – questa la terminologia di Sartre – stia a fondamento di ogni nostra relazione.
La negazione interna, nell’ottica sartriana, è quel tipo speciale di negazione che stabilisce un rapporto interno fra il ‘negato’ e il ‘negante’, in modo tale che tra i due termini s’instauri un rapporto d’essere così profondo da far sì che l’uno non possa essere compreso senza l’altro.

Il ‘nulla di separazione’ è quello scarto infinitesimale che vi è tra le due curve, l’asintoticità

Esso, allora, non indica la spazialità della relazione, ma ne è il fondamento; parimenti, la relazione tra le due curve ha come fondamento proprio quell’asintoticità intrinseca alla funzione stessa. Più precisamente, vi è asintoticità tra le due curve perché vi è un asintoto e la funzione ammette un limite che ne verifica la presenza; analogicamente, vi è un ‘nulla di separazione’ tra me e altri perché v’è un essere-per-altri, e perché il nostro rapporto fondamentale ammette un limite. Cos’è allora l’asintoto se non il ‘riferimento’ che stabilisce quel procedere d’approssimazione infinita delle due curve?
Lo sguardo altrui mi ha conferito l’oggettità, relegandomi su di un nuovo piano d’essere, il cui ‘volto’ mi sfugge, essendo per-altri e non per-me. Sartre ritiene che il legame tra me e altri si espliciti nella possibilità di essere-visto-da-lui, cioè nella possibilità permanente per un soggetto che mi vede di sostituirsi all’oggetto visto da me: l’essere-visto-da-altri come verità del vedere-altri.

Più volte il filosofo considera altri come ‘punto di fuga’, come polo in cui si alienano le mie possibilità, morendo così esse (di ‘morte sottile’) nella libertà altrui. Il punto di fuga di una retta è tecnicamente la proiezione del suo punto improprio (punto all’infinito o direzione), punto comune a tutte le rette parallele a essa. Poiché tutte le rette parallele hanno la stessa direzione, s’immagina che s’incontrino nel loro punto all’infinito; in apertura si era invece definito l’asintoto come la tangente a una curva piana in un suo punto all’infinito. Matematicamente s’intravede quindi non più di una somiglianza tra le due definizioni, ma all’interno della chiave interpretativa qui proposta – filosofica e non matematica – permettiamoci di affermarne assoluta coincidenza concettuale.
Ciascuna delle due curve è direzionata verso questo polo lontano, pertanto l’asintoto è la tangente a entrambe le curve in questo punto all’infinito. La libertà d’altri è ciò per cui esiste un essere-per-altri che mi sfugge e di cui non sono il fondamento. Sostenere che il nulla radicale è la libertà d’altri significa affermare che il nulla che mi separa dall’oggettità fuggente, conferitami da altri, è una distanza incolmabile in virtù della libertà altrui. Da ciò deriva che sfioro (quasi) quest’essere che io sono fuori di me (per-altri) senza mai raggiungerlo, come una curva asintotica a una retta. Questa chiave di lettura trova un riscontro sorprendente nello stesso testo sartriano L’essere e il nulla: «ecco che cos’è il mio me-oggetto. [...] dal punto di vista del limitato, sta ad ogni fenomeno d’ipseità come il limite matematico sta alla serie che tende verso di lui senza mai raggiungerlo: l’essere che io devo essere sta al suo limite come una curva asintotica ad una retta».
Evidentemente altri non è solo colui per il quale c’è un oggetto fuori di me, tale che io sono per-altri, senza esserne il fondamento, ma deve essere necessariamente un per-sé come lo sono io. Anche altri avverte la sua oggettità (per-me) di cui non è il fondamento: entrambi siamo due curve asintotiche tra loro.

L’asintoto è il ‘terreno’ su cui ciascuno, di volta in volta, subisce l’oggettità che è per-altri e mai per-sé: l’esplicitarsi della libertà di ciascuno

Io sono la curva asintotica alla retta (così come altri) e sono la direzione verso quel punto all’infinito in cui l’asintoto mi ‘toccherà’; allo stesso modo, la curva-altri è asintotica alla stessa retta. Ciascuno si avvicina così indefinitamente all’altro senza mai toccarlo, senza possederlo, senza assorbirlo a sé: questo, ‘per colpa’ dell’asintoticità originaria, che è il significato del reciproco essere-per-altri. Tale asintoticità è in virtù di un ‘terreno’ in cui ognuno di noi è solidificato nell’oggettità. Ma io non posso conoscermi in altri se altri è oggetto per-me e non posso nemmeno coglierlo nel suo vero essere, cioè nella sua soggettività; e lo stesso vale per lui, nei miei confronti. Pertanto, reciprocamente, «quest’Io, prodotto dall’uno e assunto dall’altro, trae la sua realtà assoluta dal fatto che è la sola separazione possibile tra due esseri sostanzialmente identici nel loro modo d’essere e che sono immediatamente presenti l’uno all’altro»: e in ciò sta il senso della loro separazione ontologica.
Tale ‘separazione’ è visivamente espressa proprio dalla discontinuità della funzione, dalla scissione in due curve, nel sorgere stesso della loro relazionalità. Altri, solo in quanto fuga – come punto improprio all’infinito della mia direzione – ‘sarà’ il punto in cui idealmente lo incontrerò. In virtù di questa direzione che io percorro, sono portato a essere, al tempo stesso, la fuga-cercante, così come altri è fuga-cercante nel suo percorso asintotico al mio. Entrambi siamo cercanti-cercati, cristallizzati, di volta in volta, in in-sé. Qui nascono i due atteggiamenti fondamentali nei confronti d’altri, comandati, per l’appunto, dall’oggetto che io sono per lui.

La conflittualità del rapportarsi all’altro si insinua in quella distanza incolmabile che ci separa (nulla di separazione). I due atteggiamenti altro non sono che la reazione originaria al nostro rapporto fondamentale, il tentativo di assorbire l’altro, di possederlo, di unirsi a lui. Ma ogni sforzo, ogni manovra è destinata all’insuccesso, poiché un’ipotetica riuscita comporterebbe la morte dell’alterità altrui. La condanna a lasciarsi sballottare indefinitamente dall’uno all’altro degli atteggiamenti fondamentali è allora la condanna della mia esistenza e di quella di ‘un altro’, al quale posso solo avvicinarmi, approssimarmi infinitesimamente senza mai coincidere, senza potergli sradicare quella libertà che gli appartiene profondamente, e senza che lui sradichi la mia.
Sopraggiunge un senso di ‘impotenza’, che esprime marcatamente l’impossibilità reciproca di cambiare direzione, deviando bruscamente il percorso asintotico di cui entrambi siamo prigionieri. Il concetto di limite matematico permette così di tirarsi fuori dall’assurdità della questione mantenendo, di contro, l’illusorietà ‘naturale’ che è propria del vano agire nei confronti d’altri.
Nella figura le due curve, insieme al proprio asintoto, sembrano toccarsi, amalgamarsi in un unicum armonioso, ma non è così e non potrà mai essere così. Questa è la verità dell’inscindibile relazione bilaterale per-sé-per-altri, in-sé; le due strutture (per-sé e per-altri) sono inseparabili poiché il per-sé rimanda al per-altri, ed è impossibile pensare che l’uno possa essere derivato dall’altro, come una conseguenza da un principio. «Senza dubbio la nostra realtà umana esige d’essere simultaneamente per-sè e per-altri [...] indissolubilmente».